本記事は数理最適化 Advent Calendar 2023の18日目の記事です。分散深層学習に使われる最適化について紹介します。
分散深層学習は、複数の計算ユニット(GPU、CPUなど)を活用して深層学習モデルを訓練する手法のことで、特にLLMのような巨大モデルの訓練には必要不可欠です。しかし、分散実行では計算量やメモリ使用量を分散させることの利点がある一方で、計算ユニット間の通信コストの増加や使用率の低下というトレードオフが存在します。したがって、単に計算資源を増やすだけではなく、深層学習モデルと計算環境に合わせた並列計算戦略の選定や計算ユニット間の通信方法のチューニングが重要です。これらのチューニング作業を時間効率的に自動化するために、最適化技術の適用が提案されています。
本記事では、分散深層学習の「並列戦略の自動化」「集団通信の低遅延化」のトピックに対して最適化がどのようにされているかにフォーカスし、代表的な研究を紹介します。
並列戦略の自動化
Alpa (2022)
- Zheng, Lianmin, et al. "Alpa: Automating inter-and Intra-Operator parallelism for distributed deep learning." 16th USENIX Symposium on Operating Systems Design and Implementation (OSDI 22). 2022.
- paper: https://www.usenix.org/system/files/osdi22-zheng-lianmin.pdf
- girthub: https://github.com/alpa-projects/alpa
Googleが提案した並列戦略の自動化手法です。Alpa自体は計算グラフの分割や計算ユニットへの割り当ても含む包括的な手法なのですが、ここでは「テンソル演算ごとにどのような並列処理を行うのか」の部分について最適化が使われているので紹介します。なお、画像は論文とブログ*1から引用しています。
この図はTransformerモデルにおける典型的な3次元の入力(activation)テンソル(左)と、パラメタのテンソル(右)を表しています。入力テンソルの[sequential, hidden]次元とパラメータ行列との積をバッチ処理で行う計算がモデルの訓練や推論時に何回も行われます。
これらのテンソルをどのように分割してテンソル積を並列計算するかには次のように任意性があります。
Data parallelとOperator parallel (type 2)の計算の様子を具体的に見てみましょう。下の図ではX,Y,Zが入力テンソル, Pがパラメタのテンソル、色付きの部分がそれぞれのDeviceがデータとして保持する行列です。
- Data Parallel(データ並列): このアプローチでは、入力テンソル(X, Y, Z)がバッチ方向に分割されます。各計算ユニットは自分自身の計算に必要なデータを保持、または計算結果として取得することで、各計算ユニットは他の計算ユニットとの通信を必要とせず、独立して並列計算を行うことができます。しかしパラメタテンソル(P)の複製は全ての計算ユニットで保持しておく必要があります。
- Operator Parallel (type 2)(オペレータ並列 ): この方法では、パラメタテンソル(P)が複数の計算ユニット間で分散して保持できるため、メモリ使用量を削減できます。しかし、計算中に計算ユニット間の通信が発生します。これは、データの一部が別の計算ユニットに存在するため、計算に必要なデータのやり取りが必要となるためです。


重要なことは、あるテンソル演算での出力は次のテンソル演算での入力になるということで、それぞれのテンソル演算で採用する並列戦略によってはOperator Parallel (type 2)のような計算ユニット間の通信を行って入力テンソルのデータ保持の形式を整える必要があります。そのため、テンソル演算での並列方針を決める際には、その演算での(1)計算量、通信量、メモリ使用量、に加えて(2)隣り合う演算間で発生する通信コストも考慮する必要があります。並列戦略はカテゴリカルであるため、まさに組み合わせ最適化問題として定式化できます。
計算時間と通信時間の総和を削減させつつ、それぞれの計算ユニットでのメモリ使用量が使用可能な量を超えないように次のように最適化問題を定式化しています。コードとしてはここで定義されています。見慣れたpulpで実装されていますね。
目的関数:

制約: s_v.T m_v <= MEM (forall v) (計算ユニットでのメモリ使用量に関する制約)
- s_v: 演算vの並列方針として何を選ぶか(バイナリ変数からなる 1-hot vector)。
- c_v: 演算vの通信コスト(定数)
- d_v: 演算vの計算コスト(定数)
- m_v: 演算vのメモリ使用量(定数)
- R_vu: (i, j)成分は演算vが並列方針s_vi、演算uが並列方針s_ujを採用した場合に、演算間で発生する通信(再配置; Resharding)コスト (定数)
変数はsであり、計算グラフの演算に対してどのような並列方法を取るのかを表現します。 目的関数は計算時間(左項)と通信時間(右項)の総和。 通信時間は隣り合う演算に対してどの並列手法を取るのかに依存するため、式としては二次形式になります。 論文ではバイナリ変数の積を線形表現化することによってILP(整数線形計画)として問題を解いています。
集団通信の最適化
集団通信は分散深層学習に欠かせない通信関数です。たとえばデータ並列であれば勾配共有のためにAllreduceという集団通信が逆伝播中に実行されます。またMoE(Mixtured of Exparts)ではAlltoall集団通信が使用されます。この集団通信に要する通信コストは決して無視できるものでなく、むしろ分散深層学習のボトルネックであると報告されています*2。
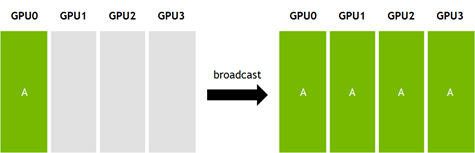
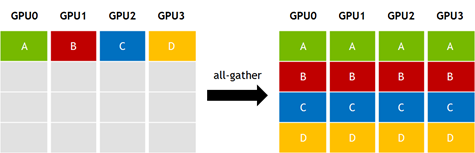
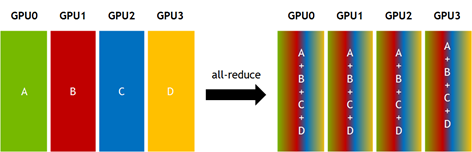
下図は集団通信であるBroadcast, Allgather, Allreduceの可視化です(画像はOperations — NCCL 2.6.4 documentationより)。
集団通信はMPI系(OpenMPI, MVAPICH, ...)やNCCL, GLOO, などの標準的な通信ライブラリで複数のアルゴリズムが実装されています。アルゴリズムはtreeやring, torusなどポピュラーなトポロジに対して効率的に動作するように設計されています。しかし、クラウドでの機械学習ジョブ実行時に不規則なネットワークリソースが割り当てられる環境や、NVIDIA DGX-1のような不規則なトポロジを持つプラットフォームで最適に機能しないことがあることが指摘されています。そのため任意のトポロジに対しても効率的に動作する集団通信アルゴリズムとは何か?の探索の試みが行われています。
BLINK (2020)
- Wang, Guanhua, et al. "Blink: Fast and generic collectives for distributed ml." Proceedings of Machine Learning and Systems 2 (2020): 172-186.
- paper: https://people.eecs.berkeley.edu/~guanhua/paper/blink-mlsys20.pdf
BLINKでは任意のトポロジに対してbroadcast型の集団通信の最適化を考えます。一つの計算ユニット(soruce)から複数の計算ユニット(destinations)にデータを分配するための効率的な通信経路を求めます。
BLINKでは全域木パッキング(Spanning Tree Packing)による定式化を提案しています。利用可能な通信資源を次のようなグラフで表現します。点が計算ユニット、枝がそれらの接続、枝の容量が通信帯域です(これが大きいほど1秒間により多くのデータを送信できる)。このグラフに対し複数の全域木をパッキングさせます。一つ一つの木がbroadcastの経路を表しており、綺麗にパッキングできれば通信資源を余すことなく使い切るbroadcastアルゴリズムを構築できる(のではないか)、という発想です。

上の図は(a)のような6つのGPUからなるトポロジに対し、3つのGPU0をsourceとする全域木に分解した様子を表しています。この全域木に従ってデータをルーティングさせることでbroadcastを行います。データを3分割し、3つの経路でbroadcastを同時に行うわけです。この場合は3つの全域木を足し合わせると元のトポロジになるため通信資源を余すところなく使い切れる、ということになります。
このようなパッキングを求める定式化は下記です。

まず全域木を列挙します(T)。列挙した全域木を番号づけし、i番目の全域木にどれほどの量のデータを流すかをw_iで表します。それぞれの枝(e)は自身の容量=通信帯域(c(e))を超える量のデータは流せません(制約(2))。
しかし全域木は与えられたグラフに対してかなり多くの個数存在するため上記の最適化問題は変数が多くなりやすく、現実的な時間では解けなくなるようです。そこで multiplicative weight update (MWU)という近似手法によって近似解の導出を行なっています。
SCCL (2021; PPoPP best paper)
- Cai, Zixian, et al. "Synthesizing optimal collective algorithms." Proceedings of the 26th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming. 2021.
- paper: https://arxiv.org/pdf/2008.08708.pdf
- github: https://github.com/microsoft/msccl-tools
Microsoftが提案する集団通信の最適化です。SCCLではSMT(SatisfiabilityModuloTheories)というSATよりも表現能力が優れた形で定式化をし、Z3(Microsoftが開発するSMTソルバ)を用いて求解します。(だからSMTで定式化した?)
この定式化では、データをチャンクと呼ばれる単位に分割し、チャンクの移動を最適化させます。
- どの計算ユニットからどの計算ユニットにチャンクを送るか
- ある計算ユニットでは、いつチャンクが送信可能になるか?
を変数で表現します。定式化はBSP(Bulk synchronous parallel)をベースに作られており、集団通信中に何回か全てのユニットで同期を行います。ユニットがあるチャンクcを送れるようになるのは前回の同期タイミングまでに受信(もしくは最初から保持する)チャンクのみです。そのようなデータ移動の整合性や集団通信の初期状態、終了状態を表す制約を追加して制約問題として定式化を行います。論文ではSMTの形式で記述されていますがILP(整数線形計画法)への変換も可能です。

(C5)のような変数積のような条件をSMTでは簡潔に書くことができます。問題の求解速度についてはSMTによる定式化をZ3ソルバで解くのと、ILPによる定式化をHiGHSソルバで解くのでほぼ同じ計算時間でした。
集団通信には通信時間(bandwidth cost)と遅延時間(latency cost)という評価観点があるのですが、この論文ではこの二つの評価項目に対し(制限付きで)パレート解を列挙する方法についても記載があります。本稿では割愛。
まとめ
分散深層学習分野に現れる最適化についていくつか紹介しました。最適化はさまざまな箇所や文脈で顔を出しますね。 他にも分散深層学習x最適化では、Beyond Data and Model Parallelism for Deep Neural Networks*3やTopoOpt: Co-optimizing Network Topology and Parallelization Strategy for Distributed Training Jobs*4などがあるので興味がある人はぜひ。