求根アルゴリズム二分法 / 割線法 [1/3]

本稿から3回に分けて様々な求根アルゴリズムを紹介したいと思います。
求根とは、ある関数 $f(x)$ の根, すなわち $f(x^*) = 0$ を満たす $x^*$ を求めることです。
もし $f$ が微分可能であれば微積分の知見を用いて根を見つけることは容易な場合も多いですが、今回は関数 $f$ が微分不可能、もしくは具体的な関数の形が分かっていない等で導関数が計算不可能な場合を想定します。このとき、数値計算の観点から関数の根の近似解を求める方法をいくつか紹介します。

二分法(Binary method)
割線法(Scant method)

まずは基本の二分法と割線法です。

二分法(Binary method)

二分法は探索区間 $[a, b$ ] を半減させながら根へと収束させる方法です。ここでいう探索区間とは根が存在するであろう範囲と同等です。たとえば関数 $f$ が連続関数でかつ, $f(a)f(b) \lt 0$ すなわち $f(a)$ と $f(b)$ の符号が異なるとき、中間値の定理より区間 $[a, b$ ] の中に根が存在することが言えます。また、この区間を初期探索区間として採用すれば二分法を用いることで、指定した精度に有限回の試行回数で収束させることが保証されています。

二分法のアルゴリズムは簡明です。

探索幅をまず2等分し
そのうち根が必ず存在するほうを次の探索幅として採用する.

input: function f
input: point a, b such that f(a)f(b) < 0 and |f(b)| < |f(a)|
constant: e 許容誤差

while |f(b)| > e
    m = (a + b) / 2
    if f(a)f(m) > 0:
        a = m 
    else:
        b = m 
    if |f(a)| < |f(b)|: # bが最適な値にする
        a, b = b, a
return b

(Python風擬似コード)

変数の持つ意味合いは以下の通り。

a: 探索区間の端点のうちbではないほう
b: 各ループ終了時における最適値
m: 二分法による新しい探索点

これは, $f(x) = (x+3)(x-1)^2$ という関数で, $a = -4, b = 0.5, e = 0.01$ として, 二分法を実行した結果となります。

利点: 収束の堅固さ(ロバスト性)
欠点: 収束の遅さ
収束次数は1です。

割線法(Scant method)

割線法は現在の探索点 $b$ と一つ前の探索点 $a$ を直線で結び, その直線と $y=0$ との交点を次の探索点とする手法です。

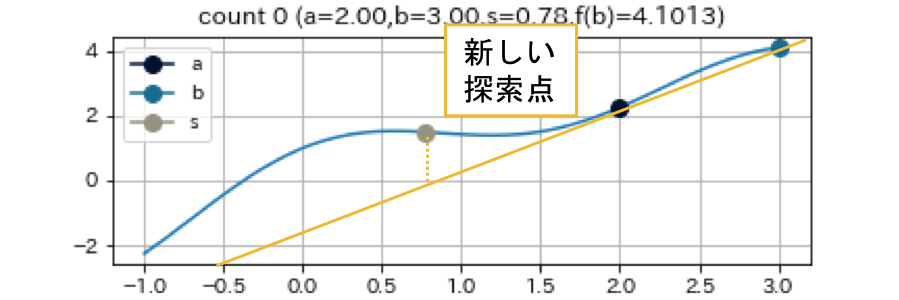
2点間での数値微分で近似した導関数によりNewton法を行うことに相当します。下で示す例からも見てとれるように, 根の周辺で関数が直線的であると非常に早く収束します。特筆すべき点として二分法とは違い, $f(a)f(b) \lt 0$ を満たす $a, b$ を求める必要はありません1。

input: function f
input: point a, b
constant: e 許容誤差

while |f(b)| > e
    s = (a*f(b)-b*f(a))/(f(b)-f(a))
    a, b = b, s
return b

a: 一つ前の探索点
b: 現在の探索点
m: 割線法による新しい探索点

なお $b$ と $a$ による直線補間と $y=0$ との交点は単純に $s = b - f(b)\cfrac{b-a}{f(b)-f(a)}$ とも書けますが, 実際には $s = \cfrac{af(b) - bf(a)}{f(b)-f(a)}$ で計算するのが推奨されています2。それは何故かというと収束が進むにつれ $b$ と $a$ は同じような値を取ることになりますが, このとき $b-a$ を計算するといわゆる桁落ちが生じてしまいます。そのとき生じる数値誤差により収束速度が遅くなってしまう恐れがあるのです。 (しかしながら, $f$ が連続関数である場合, $b$ と $a$ が近ければ, $f(b)$ と $f(a)$ も近い値になるので, 結局同じことではないかと筆者は感じている)