flopt v0.5.6; Coordinate Descent

flopt v0.5.6で座標降下法(Coordinate Descent)の実行方法を示します。

2 x² + y² + xy

の関数について、xとyの変数の片方のみを交互に移動させて局所最適解を目指します。

prob.solve(optimized_variables=[x[0]])

のようにoptimized_variablesに最適化対象の変数を指定することで、特定の変数のみを変動させます。

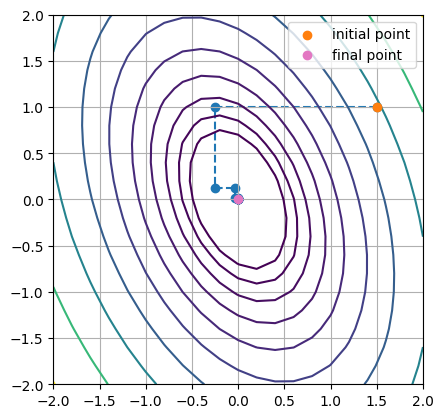
import flopt

x = flopt.Variable.array("x", 2, cat="Continuous")
x[0].setValue(1.5)
x[1].setValue(1.0)

# objective function
def f(x):
    return 2*x[0]**2 + x[1]**2 + x[0]*x[1]


prob = flopt.Problem()
prob += f(x)

# store variable path
path = [[x[0].value(), x[1].value()]]
def callback(*args, **kwargs):
    path.append([x[0].value(), x[1].value()])


# Coordinate Descent
options = dict(timelimit=0.1, callbacks=[callback])
all_log = None
for _ in range(10):
    # optimize only x_0
    status, log = prob.solve(optimized_variables=[x[0]], **options)
    all_log = log if all_log is None else all_log + log

    # optimize only x_1
    status, log = prob.solve(optimized_variables=[x[1]], **options)
    all_log = log if all_log is None else all_log + log


# plot
import numpy as np
import matplotlib.pyplot as plt

X = Y = np.linspace(-2, 2, 21)
X_mesh, Y_mesh = np.meshgrid(X, Y)
Z = f(np.array((X_mesh, Y_mesh)))

fig, ax = plt.subplots()
cmap = plt.get_cmap("tab10")

ax.contour(X, Y, Z, levels=np.logspace(-0.3, 1.2, 10))
path = np.array(path)
ax.plot(path[:,0], path[:,1], marker="o", linestyle="--", color=cmap(0), zorder=1)
ax.scatter(path[0, 0], path[0, 1], marker="o", color=cmap(1), label="initial point", zorder=2)
ax.scatter(path[-1, 0], path[-1, 1], marker="o", color=cmap(6), label="final point", zorder=2)
ax.set_aspect('equal')
ax.grid("--")
ax.legend()

プロットした結果、x軸とy軸に並行に探索点が移動している様子がわかりますね。

以下、プログラムの説明

変数の生成

長さ2の配列型の変数を生成し、初期値を設定。

import flopt

x = flopt.Variable.array("x", 2, cat="Continuous")
x[0].setValue(1.5)
x[1].setValue(1.0)

目的関数

# objective function
def f(x):
    return 2*x[0]**2 + x[1]**2 + x[0]*x[1]

問題の生成

prob = flopt.Problem()
prob += f(x)

変数列の保存用のコールバックを作成

# store variable path
path = [[x[0].value(), x[1].value()]]
def callback(*args, **kwargs):
    path.append([x[0].value(), x[1].value()])

座標降下

# Coordinate Descent
options = dict(timelimit=0.1, callbacks=[callback])
all_log = None
for _ in range(10):
    # optimize only x_0
    status, log = prob.solve(optimized_variables=[x[0]], **options)
    all_log = log if all_log is None else all_log + log

    # optimize only x_1
    status, log = prob.solve(optimized_variables=[x[1]], **options)
    all_log = log if all_log is None else all_log + log

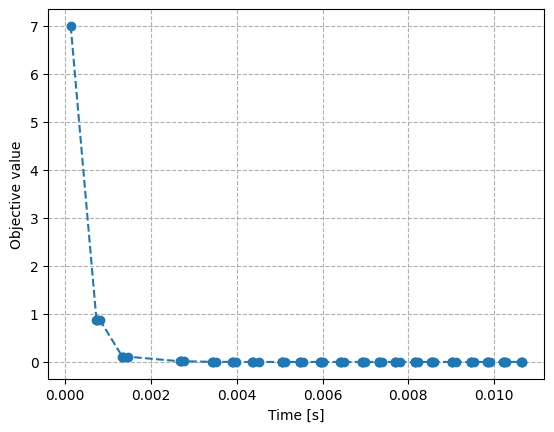
結果のプロット

all_log.plot(linestyle="--", marker="o")