csapi関数を用いて双3次スプライン関数の生成と復元を行います。
双スプラインとは2変数のスプライン関数のことです。
言い換えれば平面の補間関数になります。

まずはソースコードから。
peaksというMatlabのサンプル関数からいくつかを標本点を取り出して、双3次スプラインを行っています。
peaksはこんな形をした関数です。
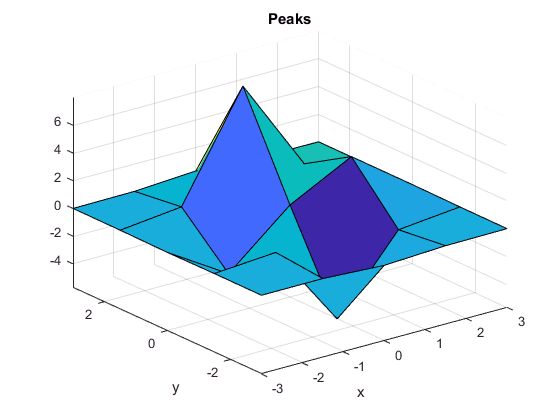
[X, Y, Z] = peaks(21);
にて、[-3, 3] * [-3, 3] をx,y軸とも21分割したメッシュ上でのpeaks関数の値を得ることができます。
% 標本点の設定 num_lattice_xs = 11; % x軸標本点個数 num_lattice_ys = 11; % y軸標本点個数 lattice_xs = linspace(-3, 3, num_lattice_xs); % x軸標本点の設定 lattice_ys = linspace(-3, 3, num_lattice_ys); % y軸標本点の設定 % 標本点上のデータの抜き出し lattice_Z = transpose(Z(1:2:end, 1:2:end));
双3次スプラインに使用する標本点として、[-3, 3] * [-3, 3]をx, y軸方向11分割したときのメッシュ上の点を使用することにします。
% 双3次スプライン補間 pp = csapi({lattice_xs, lattice_ys}, lattice_Z);
双3次スプライン関数を区分多項式pp形でcsapiから受け取けとります。
fnplt(pp)で区分多項式を可視化すると、下図のようになります。
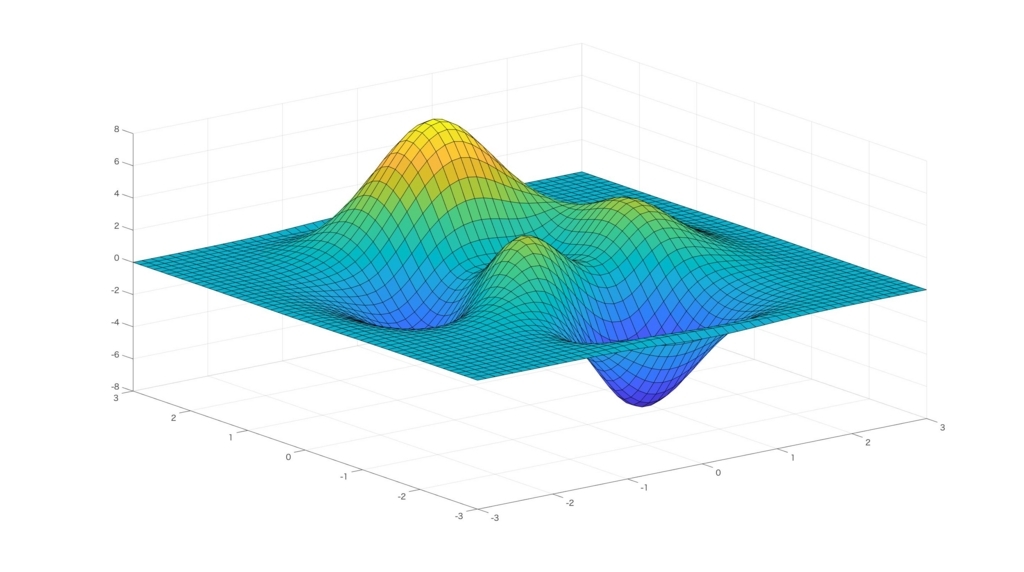
元の関数よりもかなり滑らかになっていますが、概形はそこそこ似たものになっていることが分かりますね!
補足ですが、csapiに入力する標本データ(上で言うlattice_Z)は以下のような形をしていなければなりません。

また、ある点での双3次スプライン関数の値を知りたいだけなら、fnval(pp, [x;y])を実行することで得ることができます。
標本点を以下のように荒くすると、スプライン補間も荒くなります。
% 標本点の設定 num_lattice_xs = 6; % x軸標本点個数 num_lattice_ys = 6; % y軸標本点個数 lattice_xs = linspace(-3, 3, num_lattice_xs); % x軸標本点の設定 lattice_ys = linspace(-3, 3, num_lattice_ys); % y軸標本点の設定 % 標本点上のデータの抜き出し lattice_Z = transpose(Z(1:4:end, 1:4:end));
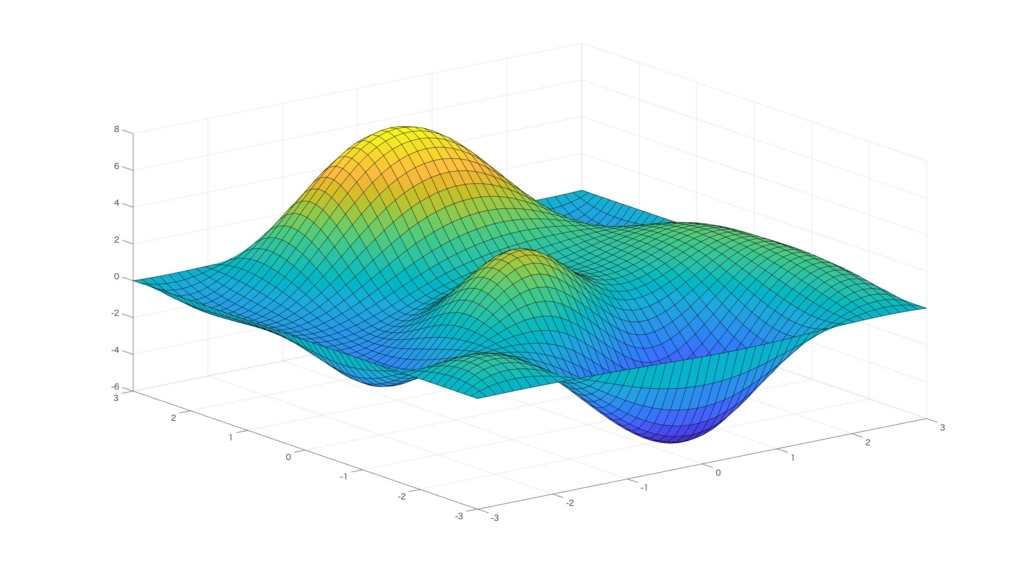
勾配を計算する必要があるなどで、双3次スプライン関数を陽な形で取り出しておく必要があるときは、ここから一工夫が必要です。
双3次スプラインは区分多項式であるため、各格子領域ごとにそれぞれ関数が定まります。
具体的には各格子領域について、スプライン関数は以下のような関数になっています。

この画像のcoefsがその下のソースコードのcoefsに対応しています。
% 双3次スプライン関数の復元 % 係数行列を整形 coefs = reshape(pp.coefs, [1, num_lattice_tqs-1, 4, num_lattice_ns-1, 4]); % 区間を指定 x_ix = 2; y_ix = 2; spline_fnc = get_fnc_from_coefs(coefs, x_ix, y_ix, lattice_xs, lattice_ys); function f = get_fnc_from_coefs(coefs, i, j, xs, ys) function fnc = get_func(x) fnc = 0; for k = 1:4 for l = 1:4 fnc = fnc + coefs(1,i,k,j,l)*(x(1)-xs(i))^(4-k)*(x(2)-ys(j))^(4-l); end end end f = @get_func; end
ハンドル関数を返す関数を書いています。
ここで一つ気をつけなければならないことがあるのですが、
x, y軸どちらかの格子区切りが3以下であるときは、このプログラムではスプライン関数を復元できません。
それはx軸格子区切り(x1, .. xm), y軸格子区切り(y1, ..., yn)の、nとmのどちらかが3以下であるとcoefsの出力形式が変わるからなのですが、
その場合の対処法について分かり次第ここに追記いたします。
matlabのcsapi関数ではde_Boorのアルゴリズムを用いて双3次スプラインを行っています。
次回はそのde_Boorのアルゴリズムを自作してみようと思います。
参考:
3 次スプライン内挿 - MATLAB csapi - MathWorks 日本
2 変数のサンプル関数 - MATLAB peaks - MathWorks 日本
https://jp.mathworks.com/matlabcentral/answers/77100-reconstruct-multivariate-spline-from-csapi