これの後編です。
実際に簡単な関数でいくつか補間による近似を行なってみたいと思います。

fが近似したい関数、gがデータ点(0, 0) (1, 1) (2, 2)から構成した差分商補間になります。
fは2次式でかつ、前編の最後の定理「剰余なしのn項からなるNewtonの差分商補間はn-1次の多項式について厳密である」より、重複しない3つのデータ点から差分商補間を構成しているので、厳密に近似できたということになります。

これはf = x3を3つのデータ点(0, 0) (1, 1), (2, 8)から補間した例です。
3次式なのでデータ点が4つあれば厳密になります。
次はlog2を近似した結果です。
補間点を(1, log1), (2, log2), (3, log3), ...と一つずつ増やしていった時に、補間の精度が徐々に上がっていく様子をアニメーションにしてみました。
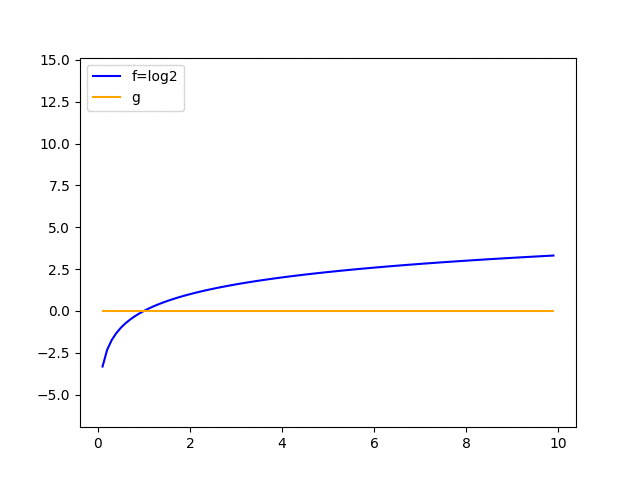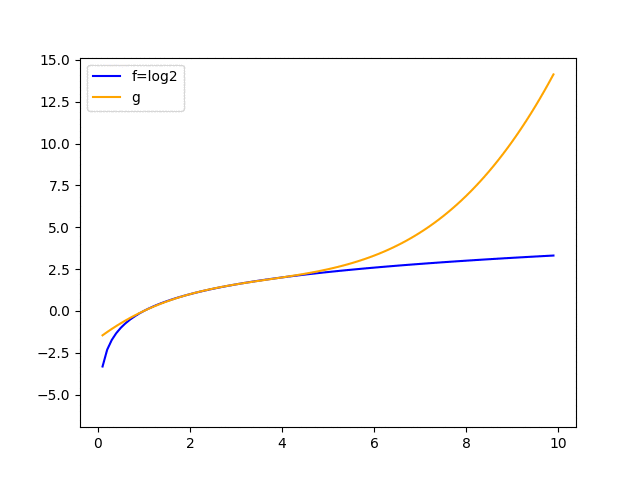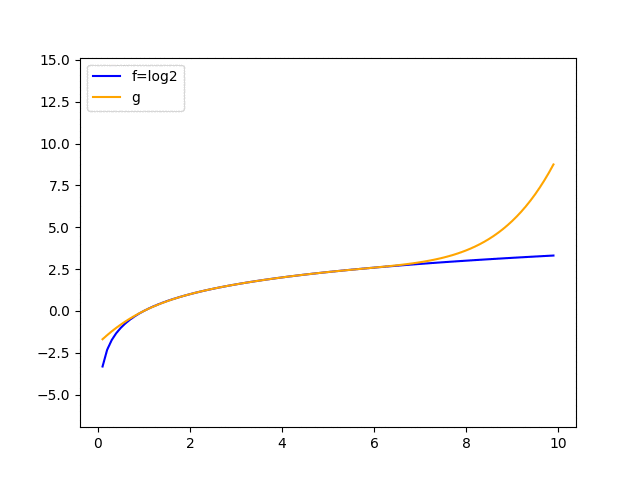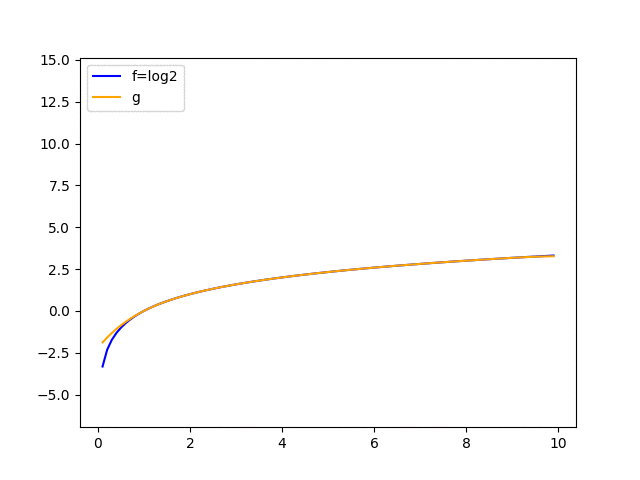
局所的にはいい精度で近似を行えていますね。
最後はステップ関数ceil(x)の例になります。
近似したい関数が微分可能でなくても差分商は計算できるため、不連続はステップ関数でも差分商近似を適用できます(できるはず)。

まぁうまくいっていませんね笑。