
上記のグラフのstartからgoalまでの最短路を求めたいとします。 (グラフの枝の重みは枝の長さ)
直感的には、startとgoalから離れた点や枝を考える必要はない(i.e.最短路にそれらの点や枝が含まれることがない)ように思えますが、それをどう厳密に表現するか?という話になります。
今回は楕円を用いてそのような最短路に絶対含まれることがない枝を探索します。 まず、startからgoalまでの道を一つ見つけます。
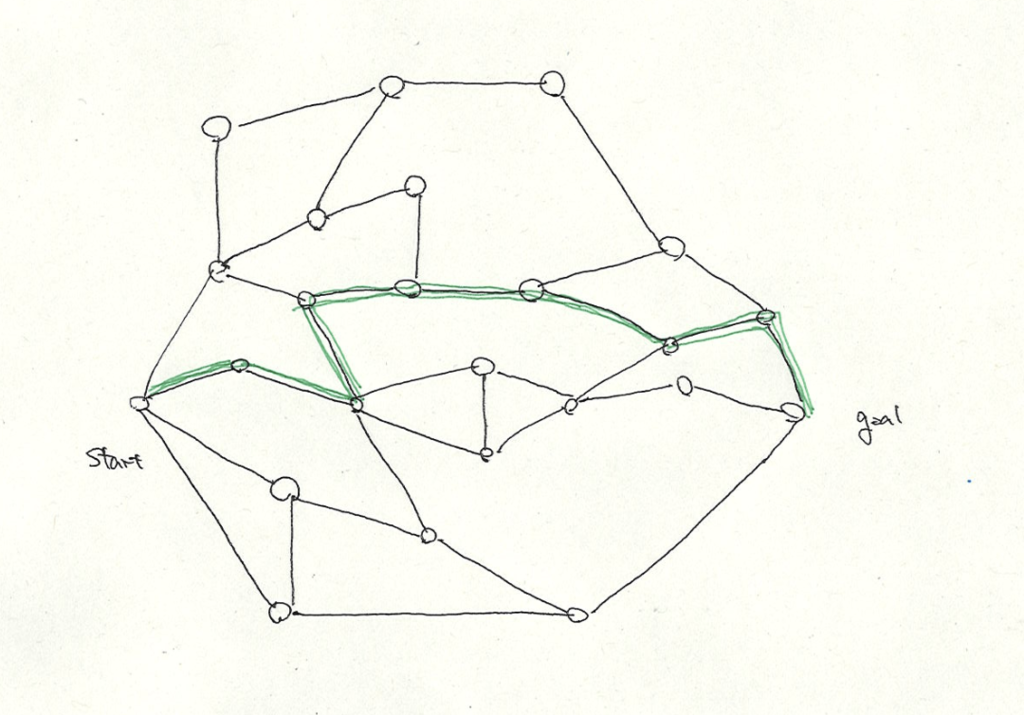
図中緑色の道を見つけたとします。(このとき、このパスが最短路である必要はありません)
次に長軸が「startとgoalを通り、長さが上で見つけたパス長」で、startとgoalが焦点であるような楕円を考えます。

このとき、startとgoalを結ぶ最短路はこの楕円の中に含まれています。(理由は後ほど)
逆に言えば、この楕円の外、もしくはこの楕円を横切るような点や枝は最短路には含まれていないことになります。(例えば下図、バツ印)

そのような点や枝を取り除くと以下のようにグラフを小さくすることができます。

上の例では、それほど削れていませんが、グラフが大きくなればなるほど削れる枝が多くなり、より効率的に最短路を探索できることになります。
さて、ではなぜstartとgoalを結ぶ最短路はこの楕円の中に含まれていると言えるのかというと、これは楕円の性質に依るものです。 楕円の性質(というよりはむしろ定義)により「楕円上の任意の点について、二つの焦点との距離の和は一定で、それは長軸の長さと等しい」ということが成り立ちます。
よって、この場合については、楕円上の任意の点について、startとgoalとの距離の和は、最初に見つけてきたパスの長さに等しいということが分かります。 これより、楕円の外に出るようなstart-goal間の道については、最初に見つけてきたパスの長さよりも確実に長くなることになるので、start-goal間の最短経路は必ず楕円の中に含まれることが言えるのです。