次のようなネットワークのフロー分解を考えます。

まず、フローとは何かという話ですが、
始点(図s)から終点に(図t)に水を流すことを考えます。
そのときの"水の流れ"のことをフローと呼びますが、それにはいくつか条件があります。
図のノード(丸)とノードを結ぶ矢印の方向に管があり、それを伝って矢印の方向に水が流れるのですが、それぞれの管に流せる水の最大量が決まって、管に流せる量よりも多くの水は流せません。
またそのときにs, t以外のノード(図1~4)では
水の流入量と流出量が等しくなってなければなりません。(例えばノード1では流入量は3 + 2 = 5で流出量は1 + 4 = 5)
以上の性質を満たすものがフローと呼ばれるものです。
そこで、そのフローをsからtへのパス、もしくはグラフ中の閉路に一定量の水を流すフローに分解しようというのがフローの分解になります。
結果からいうと、上図のネットワークは以下のように分解されます。
(見にくかったら、ごめんなさい)

左上のフローを右の5つのフローに分解しています。
分解の方法はいたってシンプルです。
アルゴリズム
- sからtへのパスまたは閉路を見つける
- 1で見つけたパスまたは閉路
の全ての辺について、最小の流水量をdとおくについて- 閉路であれば, 全ての辺の最小の流水量をdとおく
- パスであれば, 全ての辺の最小の流水量, 始点からの総出量, 終点への総入量の中で最小のものをdとおく注1
- 1で見つけたパスまたは閉路の全ての辺にdだけ水を流すフローを保存(これが分解の要素の一つ)
- 元のグラフから3のフローを引く
- sからtへのパスまたは閉路がなくなれば、終了。そうでなければ1に戻る
実際に計算してみましょう。元のネットワークから実際にアルゴリズムを辿っていくと、

①sからtへのパスまたは閉路を見つける

② ①で見つけたパスまたは閉路の全ての辺について、最小の流水量を計算しdとおく
③ ①で見つけたパスまたは閉路の全ての辺にdだけ水を流すフローを保存(これが分解の要素の一つ)
d = 1

④ 元のグラフから③のフローを引く

④ 終了後のグラフ 流水量0のエッジを削除した

⑤ ①に戻る
①sからtへのパスまたは閉路を見つける

② ①で見つけたパスまたは閉路の全ての辺について、最小の流水量を計算しdとおく
③ ①で見つけたパスまたは閉路の全ての辺にdだけ水を流すフローを保存(これが分解の要素の一つ)
d = 2

④ 元のグラフから③のフローを引く

⑤ ①に戻る
①sからtへのパスまたは閉路を見つける

② ①で見つけたパスまたは閉路の全ての辺について、最小の流水量を計算しdとおく
③ ①で見つけたパスまたは閉路の全ての辺にdだけ水を流すフローを保存(これが分解の要素の一つ)
d = 2

④ 元のグラフから③のフローを引く

⑤ ①に戻る
①sからtへのパスまたは閉路を見つける

② ①で見つけたパスまたは閉路の全ての辺について、最小の流水量を計算しdとおく
③ ①で見つけたパスまたは閉路の全ての辺にdだけ水を流すフローを保存(これが分解の要素の一つ)
d = 1
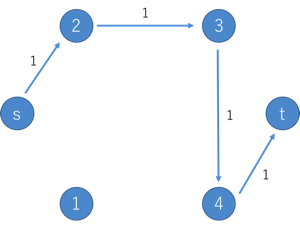
④ 元のグラフから③のフローを引く

⑤ ①に戻る
①sからtへのパスまたは閉路を見つける

② ①で見つけたパスまたは閉路の全ての辺について、最小の流水量を計算しdとおく
③ ①で見つけたパスまたは閉路の全ての辺にdだけ水を流すフローを保存(これが分解の要素の一つ)
d = 1

④ 元のグラフから③のフローを引く
⑤ アルゴリズム終了
なぜこのアルゴリズムが上手くいくのかというと、
「フローからフローを引いてもフローです」(五七五)ということですね。
更新 : 2018/11/3
2. 1で見つけたパスまたは閉路の全ての辺について、最小の流水量をdとおく
↓ 変更
2. 1で見つけたパスまたは閉路について
- 閉路であれば, 全ての辺の最小の流水量をdとおく
- パスであれば, 全ての辺の最小の流水量, 始点からの総出量, 終点への総入量の中で最小のものをdとおく
変更前では, 分解がうまくいかない例があります。

例えば, ここでsからtへの1辺からなるパスを見つけて, フロー2を流すと, 元々のネットワークは

このように更新され, sからtへのフローではなくなってしまいました。
変更後の方法では, sからtへの1辺からなるパスを見つけると, sからの総出量, tへの総出量はそれぞれ1なので, このパスにフロー1が流れることになります。すると, 更新後のネットワークはフロー量1の閉路となり, うまく分解できました。
